Metoda trapezului

Aspecte teoretice:

Aproximarea numerică a valorii unei integrale definite folosind formula trapezului. Considerăm o funcție reală f, continuă pe intervalul [a; b]. Dacă se cunoaște o primitivă a sa, F(x), atunci integrala definită a lui f(x) între limitele [a; b] se poate calcula folosind formula lui Leibniz-Newton:

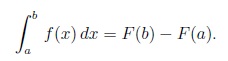
Pentru o serie de funcții a căror expresie analitică este cunoscută, calculul integralei se poate efectua folosind formule cunoscute. În practică, există numeroase situații în care evaluarea unei integrale definite cu metode analitice cunoscute este foarte complicată sau chiar imposibil de realizat. De exemplu, dacă expresia analitică a funcției f este necunoscută, valorile acesteia fiind doar tabelate, nici nu se poate vorbi despre o primitivă a acesteia. Sau, există situații când expresia analitică a funcției f este foarte complicată și determinarea unei primitive ar fi greoaie sau chiar nu poate fi determinată pe căi elementare, analitice. Există funcții ale căror primitive, deși există, nu pot fi exprimate prin funcții elementare. În aceste situații, calculul integralei definite nu mai poate fi făcut cu relația anterioară și se recurge la metode numerice de aproximare.
În continuare prezentăm calculul valorii unei integrale definite folosind metoda Divide et Impera și bazându-ne pe una dintre metodele de aproximare numită metoda trapezului. Tehnica Divide et Impera presupune împărțirea intervalului [a; b] în două jumătăți. Se aplică formula cunoscută

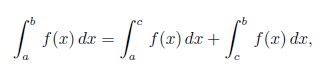unde c = (a + b)/2 este mijlocul intervalului [a; b]. Procedeul se repetă, până când lungimea intervalului devine suficient de mică, b – a < ε, cu ε = 0,0001, de exemplu. În acest caz elementar, curba funcției de integrat (pe intervalul [a; b], de lungime ε), se aproximează liniar prin dreapta ce trece prin punctele (a; f(a)) și (b; f(b)). Așadar, valoarea integralei definite a lui f între limitele [a; b] se aproximează prin aria trapezului cu vârfurile (a; 0), (b; 0) (a; f(a)) și (b; f(b)). Deci

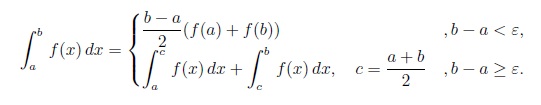Implementare:

Cod Sursa C++

// MetodaTrapezuluiCPP.cpp : Defines the entry point for the console application.
//
 
#include "stdafx.h"
#include 
#define eps 0.0001
 
using namespace std;
 
double func1(double x)
{
	return x;
}
 
double func2(double x)
{
	return exp(-x*x);
}
 
double func3(double x)
{
	return pow(x, x);
}
 
double calculIntegrala(double a, double b, double(*f)(double))
{
	if ((b - a) < eps)
		return (b - a)*((*f)(a)+(*f)(b)) / 2.0;
	else
	{
		double c = (a + b) / 2.0;
		return calculIntegrala(a, c, f) + calculIntegrala(c, b, f);
	}
}
 
int main()
{
	double a, b, l, aux;
	cout << "Capatul stang al intervalului de integrare: ";
	cin >> a;
	cout << "Capatul drept al intervalului de integrare: ";
	cin >> b;
	if (b < a)
	{
		aux = a;
		a = b;
		b = aux;
	}
	l = calculIntegrala(a, b, &func3); //la fel pentru func1, func2
	cout << "Valoarea integralei definite a functiei intre limitele [" << a << "," << b << "] este " << l << endl;
	system("pause");
}

Rezultat: